Dutch people are known for splitting their bills. When frequently eating with the same group this could normally lead to an awkward situation, where everybody has to pay everybody a little bit. Most students use the site “https://wiebetaaltwat.nl/”. You create a group with the people you frequently eat with, and every time you do something with a set of these people you add your expense to the list.
Once in a while you want your bills paid, to do this wiebetaaltwat tries to find a way in which there is the lowest amount of transactions. Last week I had a discussion with a friend about what would be the best way to calculate these transactions. This post will show my first attempt at finding an algorithm, why my algorithm was wrong, and how I improved it.
My first idea was:
- Input: a list L with the amount every person has to pay
- Returns: amount of transactions
- Define variable transaction_count
- while there is still an amount left:
- Sort L
- Let the person who has to pay the most (last element of L) pay to the person who has to get the most (first element of L)
- transaction_count +=1
- return transaction_count
Now every step either:
- Both amounts cancel each other
- The one who paid has no debt anymore
- The one who got money got everything he had to get
This guarantees that we take a maximum of N-1 transactions (which is pretty cool). Let’s analyse the complexity of this algorithm:
- The initial sorting takes n*log(n)
- One transaction calculation is O(1) (a step we have to take n times)
- Inserting the leftover value is log(n) (a step we have to take n times)
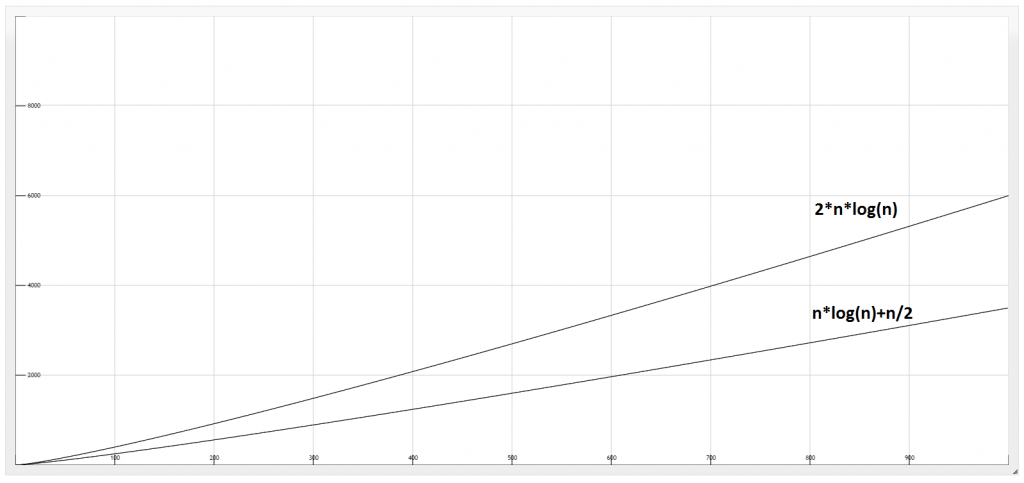
So this program has a complexity of n*log(n), it takes exactly n*log(n) + n/2 steps.
I programmed this out in Python to show that the approach works:
My friend wasn’t convinced by this script simply saying that it isn’t a good “real world example”. After a few hours I came up with an example that is NOT solved efficiently by my script:
| Person | Anna | Bob | Charlie | Dennis | Elisabeth |
|---|---|---|---|---|---|
| Initial money: | 35 | 34 | -2 | -33 | -34 |
| E pays A | 1 | 34 | -2 | -33 | 0 |
| D pays B | 1 | 1 | -2 | 0 | 0 |
| C pays A | 0 | 1 | -1 | 0 | 0 |
| C pays B | 0 | 0 | 0 | 0 | 0 |
How it should have been solved:
| Person | Anna | Bob | Charlie | Dennis | Elisabeth |
|---|---|---|---|---|---|
| Initial money: | 35 | 34 | -2 | -33 | -34 |
| E pays C | 35 | 0 | -2 | -33 | 0 |
| D pays A | 2 | 0 | -2 | 0 | 0 |
| C pays A | 0 | 0 | 0 | 0 | 0 |
| Nothing!! | 0 | 0 | 0 | 0 | 0 |
As you can see by searching for the same value the amount of transactions can be reduced.
An observation we make is that this is done by removing values (a,b) where a==-b.
To do this we:
- Before each step, take a as the last element of L and b as the first element of L. Check if -a or -b is in L. If this is the case, merge these two.
Searching for two numbers in a list takes 2*log(n). With this update the total steps we take is n*log(n) + n/2 * 2 * log(n) which is 2*n*log(n).
I plotted the two graphs so you can see that the optimal solution takes double the time than my first solution:
Is my second algorithm correct? Is there a way to calculate who has to pay what which leads to less transactions? I hope so! If you have a better algorithm, please leave a comment!